Find Merge Point of Two Lists Hackerrank Solution C++
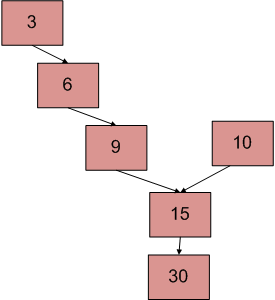
There are two singly linked lists in a system. By some programming error, the end node of one of the linked list got linked to the second list, forming an inverted Y shaped list. Write a program to get the point where two linked list merge.
Become a success story instead of just reading about them. Prepare for coding interviews at Amazon and other top product-based companies with our Amazon Test Series. Includes topic-wise practice questions on all important DSA topics along with 10 practice contests of 2 hours each. Designed by industry experts that will surely help you practice and sharpen your programming skills. Wait no more, start your preparation today!
Above diagram shows an example with two linked list having 15 as intersection point.
Method 1(Simply use two loops)
Use 2 nested for loops. The outer loop will be for each node of the 1st list and inner loop will be for 2nd list. In the inner loop, check if any of nodes of the 2nd list is same as the current node of the first linked list. The time complexity of this method will be O(M * N) where m and n are the numbers of nodes in two lists.
Method 2 (Mark Visited Nodes)
This solution requires modifications to basic linked list data structure. Have a visited flag with each node. Traverse the first linked list and keep marking visited nodes. Now traverse the second linked list, If you see a visited node again then there is an intersection point, return the intersecting node. This solution works in O(m+n) but requires additional information with each node. A variation of this solution that doesn't require modification to the basic data structure can be implemented using a hash. Traverse the first linked list and store the addresses of visited nodes in a hash. Now traverse the second linked list and if you see an address that already exists in the hash then return the intersecting node.
Method 3(Using difference of node counts)
- Get count of the nodes in the first list, let count be c1.
- Get count of the nodes in the second list, let count be c2.
- Get the difference of counts d = abs(c1 – c2)
- Now traverse the bigger list from the first node till d nodes so that from here onwards both the lists have equal no of nodes
- Then we can traverse both the lists in parallel till we come across a common node. (Note that getting a common node is done by comparing the address of the nodes)
Below image is a dry run of the above approach:

Below is the implementation of the above approach :
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public :
int data;
Node* next;
};
int getCount(Node* head);
int _getIntesectionNode( int d, Node* head1, Node* head2);
int getIntesectionNode(Node* head1, Node* head2)
{
int c1 = getCount(head1);
int c2 = getCount(head2);
int d;
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
int _getIntesectionNode( int d, Node* head1, Node* head2)
{
Node* current1 = head1;
Node* current2 = head2;
for ( int i = 0; i < d; i++) {
if (current1 == NULL) {
return -1;
}
current1 = current1->next;
}
while (current1 != NULL && current2 != NULL) {
if (current1 == current2)
return current1->data;
current1 = current1->next;
current2 = current2->next;
}
return -1;
}
int getCount(Node* head)
{
Node* current = head;
int count = 0;
while (current != NULL) {
count++;
current = current->next;
}
return count;
}
int main()
{
Node* newNode;
Node* head1 = new Node();
head1->data = 10;
Node* head2 = new Node();
head2->data = 3;
newNode = new Node();
newNode->data = 6;
head2->next = newNode;
newNode = new Node();
newNode->data = 9;
head2->next->next = newNode;
newNode = new Node();
newNode->data = 15;
head1->next = newNode;
head2->next->next->next = newNode;
newNode = new Node();
newNode->data = 30;
head1->next->next = newNode;
head1->next->next->next = NULL;
cout << "The node of intersection is " << getIntesectionNode(head1, head2);
}
C
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
int getCount( struct Node* head);
int _getIntesectionNode( int d, struct Node* head1, struct Node* head2);
int getIntesectionNode( struct Node* head1, struct Node* head2)
{
int c1 = getCount(head1);
int c2 = getCount(head2);
int d;
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
int _getIntesectionNode( int d, struct Node* head1, struct Node* head2)
{
int i;
struct Node* current1 = head1;
struct Node* current2 = head2;
for (i = 0; i < d; i++) {
if (current1 == NULL) {
return -1;
}
current1 = current1->next;
}
while (current1 != NULL && current2 != NULL) {
if (current1 == current2)
return current1->data;
current1 = current1->next;
current2 = current2->next;
}
return -1;
}
int getCount( struct Node* head)
{
struct Node* current = head;
int count = 0;
while (current != NULL) {
count++;
current = current->next;
}
return count;
}
int main()
{
struct Node* newNode;
struct Node* head1 = ( struct Node*) malloc ( sizeof ( struct Node));
head1->data = 10;
struct Node* head2 = ( struct Node*) malloc ( sizeof ( struct Node));
head2->data = 3;
newNode = ( struct Node*) malloc ( sizeof ( struct Node));
newNode->data = 6;
head2->next = newNode;
newNode = ( struct Node*) malloc ( sizeof ( struct Node));
newNode->data = 9;
head2->next->next = newNode;
newNode = ( struct Node*) malloc ( sizeof ( struct Node));
newNode->data = 15;
head1->next = newNode;
head2->next->next->next = newNode;
newNode = ( struct Node*) malloc ( sizeof ( struct Node));
newNode->data = 30;
head1->next->next = newNode;
head1->next->next->next = NULL;
printf ( "\n The node of intersection is %d \n" ,
getIntesectionNode(head1, head2));
getchar ();
}
Java
class LinkedList {
static Node head1, head2;
static class Node {
int data;
Node next;
Node( int d)
{
data = d;
next = null ;
}
}
int getNode()
{
int c1 = getCount(head1);
int c2 = getCount(head2);
int d;
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
int _getIntesectionNode( int d, Node node1, Node node2)
{
int i;
Node current1 = node1;
Node current2 = node2;
for (i = 0 ; i < d; i++) {
if (current1 == null ) {
return - 1 ;
}
current1 = current1.next;
}
while (current1 != null && current2 != null ) {
if (current1.data == current2.data) {
return current1.data;
}
current1 = current2;
current2 = current2.next;
}
return - 1 ;
}
int getCount(Node node)
{
Node current = node;
int count = 0 ;
while (current != null ) {
count++;
current = current.next;
}
return count;
}
public static void main(String[] args)
{
LinkedList list = new LinkedList();
list.head1 = new Node( 3 );
list.head1.next = new Node( 6 );
list.head1.next.next = new Node( 9 );
list.head1.next.next.next = new Node( 15 );
list.head1.next.next.next.next = new Node( 30 );
list.head2 = new Node( 10 );
list.head2.next = new Node( 15 );
list.head2.next.next = new Node( 30 );
System.out.println( "The node of intersection is " + list.getNode());
}
}
Python3
class Node:
def __init__( self ,data):
self .data = data
self . next = None
def getIntersectionNode(head1,head2):
c1 = getCount(head1)
c2 = getCount(head2)
if c1 > c2:
d = c1 - c2
return _getIntersectionNode(d,head1,head2)
else :
d = c2 - c1
return _getIntersectionNode(d,head2,head1)
def _getIntersectionNode(d,head1,head2):
current1 = head1
current2 = head2
for i in range (d):
if current1 is None :
return - 1
current1 = current1. next
while current1 is not None and current2 is not None :
if current1 is current2:
return current1.data
current1 = current1. next
current2 = current2. next
return - 1
def getCount(node):
cur = node
count = 0
while cur is not None :
count + = 1
cur = cur. next
return count
if __name__ = = '__main__' :
common = Node( 15 )
head1 = Node( 3 )
head1. next = Node( 6 )
head1. next . next = Node( 9 )
head1. next . next . next = common
head1. next . next . next . next = Node( 30 )
head2 = Node( 10 )
head2. next = common
head2. next . next = Node( 30 )
print ( "The node of intersection is " ,getIntersectionNode(head1,head2))
C#
using System;
class LinkedList {
Node head1, head2;
public class Node {
public int data;
public Node next;
public Node( int d)
{
data = d;
next = null ;
}
}
int getNode()
{
int c1 = getCount(head1);
int c2 = getCount(head2);
int d;
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
int _getIntesectionNode( int d, Node node1, Node node2)
{
int i;
Node current1 = node1;
Node current2 = node2;
for (i = 0; i < d; i++) {
if (current1 == null ) {
return -1;
}
current1 = current1.next;
}
while (current1 != null && current2 != null ) {
if (current1.data == current2.data) {
return current1.data;
}
current1 = current1.next;
current2 = current2.next;
}
return -1;
}
int getCount(Node node)
{
Node current = node;
int count = 0;
while (current != null ) {
count++;
current = current.next;
}
return count;
}
public static void Main(String[] args)
{
LinkedList list = new LinkedList();
list.head1 = new Node(3);
list.head1.next = new Node(6);
list.head1.next.next = new Node(9);
list.head1.next.next.next = new Node(15);
list.head1.next.next.next.next = new Node(30);
list.head2 = new Node(10);
list.head2.next = new Node(15);
list.head2.next.next = new Node(30);
Console.WriteLine( "The node of intersection is " + list.getNode());
}
}
Javascript
<script>
class Node
{
constructor(item)
{
this .data=item;
this .next= null ;
}
}
let head1,head2;
function getNode()
{
let c1 = getCount(head1);
let c2 = getCount(head2);
let d;
if (c1 > c2) {
d = c1 - c2;
return _getIntesectionNode(d, head1, head2);
}
else {
d = c2 - c1;
return _getIntesectionNode(d, head2, head1);
}
}
function _getIntesectionNode(d,node1,node2)
{
let i;
let current1 = node1;
let current2 = node2;
for (i = 0; i < d; i++) {
if (current1 == null ) {
return -1;
}
current1 = current1.next;
}
while (current1 != null && current2 != null ) {
if (current1.data == current2.data) {
return current1.data;
}
current1 = current1.next;
current2 = current2.next;
}
return -1;
}
function getCount(node)
{
let current = node;
let count = 0;
while (current != null ) {
count++;
current = current.next;
}
return count;
}
head1 = new Node(3);
head1.next = new Node(6);
head1.next.next = new Node(9);
head1.next.next.next = new Node(15);
head1.next.next.next.next = new Node(30);
head2 = new Node(10);
head2.next = new Node(15);
head2.next.next = new Node(30);
document.write( "The node of intersection is " + getNode());
</script>
Output
The node of intersection is 15
Time Complexity: O(m+n)
Auxiliary Space: O(1)
Method 4(Make circle in first list)
Thanks to Saravanan Man for providing below solution.
1. Traverse the first linked list(count the elements) and make a circular linked list. (Remember the last node so that we can break the circle later on).
2. Now view the problem as finding the loop in the second linked list. So the problem is solved.
3. Since we already know the length of the loop(size of the first linked list) we can traverse those many numbers of nodes in the second list, and then start another pointer from the beginning of the second list. we have to traverse until they are equal, and that is the required intersection point.
4. remove the circle from the linked list.
Time Complexity: O(m+n)
Auxiliary Space: O(1)
Method 5 (Reverse the first list and make equations)
Thanks to Saravanan Mani for providing this method.
1) Let X be the length of the first linked list until intersection point. Let Y be the length of the second linked list until the intersection point. Let Z be the length of the linked list from the intersection point to End of the linked list including the intersection node. We Have X + Z = C1; Y + Z = C2; 2) Reverse first linked list. 3) Traverse Second linked list. Let C3 be the length of second list - 1. Now we have X + Y = C3 We have 3 linear equations. By solving them, we get X = (C1 + C3 – C2)/2; Y = (C2 + C3 – C1)/2; Z = (C1 + C2 – C3)/2; WE GOT THE INTERSECTION POINT. 4) Reverse first linked list.
Advantage: No Comparison of pointers.
Disadvantage: Modifying linked list(Reversing list).
Time complexity: O(m+n)
Auxiliary Space: O(1)
Method 6 (Traverse both lists and compare addresses of last nodes) This method is only to detect if there is an intersection point or not. (Thanks to NeoTheSaviour for suggesting this)
1) Traverse the list 1, store the last node address 2) Traverse the list 2, store the last node address. 3) If nodes stored in 1 and 2 are same then they are intersecting.
The time complexity of this method is O(m+n) and used Auxiliary space is O(1)
Method 7 (Use Hashing)
Basically, we need to find a common node of two linked lists. So we hash all nodes of the first list and then check the second list.
1) Create an empty hash set.
2) Traverse the first linked list and insert all nodes' addresses in the hash set.
3) Traverse the second list. For every node check if it is present in the hash set. If we find a node in the hash set, return the node.
Java
import java.util.*;
class Node {
int data;
Node next;
Node( int d)
{
data = d;
next = null ;
}
}
class LinkedListIntersect {
public static void main(String[] args)
{
Node n1 = new Node( 1 );
n1.next = new Node( 2 );
n1.next.next = new Node( 3 );
n1.next.next.next = new Node( 4 );
n1.next.next.next.next = new Node( 5 );
n1.next.next.next.next.next = new Node( 6 );
n1.next.next.next.next.next.next = new Node( 7 );
Node n2 = new Node( 10 );
n2.next = new Node( 9 );
n2.next.next = new Node( 8 );
n2.next.next.next = n1.next.next.next;
Print(n1);
Print(n2);
System.out.println(MegeNode(n1, n2).data);
}
public static void Print(Node n)
{
Node cur = n;
while (cur != null ) {
System.out.print(cur.data + " " );
cur = cur.next;
}
System.out.println();
}
public static Node MegeNode(Node n1, Node n2)
{
HashSet<Node> hs = new HashSet<Node>();
while (n1 != null ) {
hs.add(n1);
n1 = n1.next;
}
while (n2 != null ) {
if (hs.contains(n2)) {
return n2;
}
n2 = n2.next;
}
return null ;
}
}
Python3
class Node :
def __init__( self , d):
self .data = d;
self . next = None ;
def Print (n):
cur = n;
while (cur ! = None ) :
print (cur.data, end = " " );
cur = cur. next ;
print ("");
def MegeNode(n1, n2):
hs = set ();
while (n1 ! = None ):
hs.add(n1);
n1 = n1. next ;
while (n2 ! = None ):
if (n2 in hs):
return n2;
n2 = n2. next ;
return None ;
n1 = Node( 1 );
n1. next = Node( 2 );
n1. next . next = Node( 3 );
n1. next . next . next = Node( 4 );
n1. next . next . next . next = Node( 5 );
n1. next . next . next . next . next = Node( 6 );
n1. next . next . next . next . next . next = Node( 7 );
n2 = Node( 10 );
n2. next = Node( 9 );
n2. next . next = Node( 8 );
n2. next . next . next = n1. next . next . next ;
Print (n1);
Print (n2);
print (MegeNode(n1, n2).data);
C#
using System;
using System.Collections.Generic;
public class Node
{
public int data;
public Node next;
public Node( int d)
{
data = d;
next = null ;
}
}
public class LinkedListIntersect
{
public static void Main(String[] args)
{
Node n1 = new Node(1);
n1.next = new Node(2);
n1.next.next = new Node(3);
n1.next.next.next = new Node(4);
n1.next.next.next.next = new Node(5);
n1.next.next.next.next.next = new Node(6);
n1.next.next.next.next.next.next = new Node(7);
Node n2 = new Node(10);
n2.next = new Node(9);
n2.next.next = new Node(8);
n2.next.next.next = n1.next.next.next;
Print(n1);
Print(n2);
Console.WriteLine(MegeNode(n1, n2).data);
}
public static void Print(Node n)
{
Node cur = n;
while (cur != null )
{
Console.Write(cur.data + " " );
cur = cur.next;
}
Console.WriteLine();
}
public static Node MegeNode(Node n1, Node n2)
{
HashSet<Node> hs = new HashSet<Node>();
while (n1 != null )
{
hs.Add(n1);
n1 = n1.next;
}
while (n2 != null )
{
if (hs.Contains(n2))
{
return n2;
}
n2 = n2.next;
}
return null ;
}
}
Javascript
<script>
class Node
{
constructor(d)
{
this .data = d;
this .next = null ;
}
}
function Print(n)
{
let cur = n;
while (cur != null )
{
document.write(cur.data + " " );
cur = cur.next;
}
document.write( "<br>" );
}
function MegeNode(n1, n2)
{
let hs = new Set();
while (n1 != null )
{
hs.add(n1);
n1 = n1.next;
}
while (n2 != null )
{
if (hs.has(n2))
{
return n2;
}
n2 = n2.next;
}
return null ;
}
let n1 = new Node(1);
n1.next = new Node(2);
n1.next.next = new Node(3);
n1.next.next.next = new Node(4);
n1.next.next.next.next = new Node(5);
n1.next.next.next.next.next = new Node(6);
n1.next.next.next.next.next.next = new Node(7);
let n2 = new Node(10);
n2.next = new Node(9);
n2.next.next = new Node(8);
n2.next.next.next = n1.next.next.next;
Print(n1);
Print(n2);
document.write(MegeNode(n1, n2).data);
</script>
Output
1 2 3 4 5 6 7 10 9 8 4 5 6 7 4
This method required O(n) additional space and not very efficient if one list is large.
Method 8( 2-pointer technique ):
Using Two pointers :
- Initialize two pointers ptr1 and ptr2 at the head1 and head2.
- Traverse through the lists,one node at a time.
- When ptr1 reaches the end of a list, then redirect it to the head2.
- similarly when ptr2 reaches the end of a list, redirect it the head1.
- Once both of them go through reassigning, they will be equidistant from
the collision point - If at any node ptr1 meets ptr2, then it is the intersection node.
- After second iteration if there is no intersection node it returns NULL.
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public :
int data;
Node* next;
};
Node* intersectPoint(Node* head1, Node* head2)
{
Node* ptr1 = head1;
Node* ptr2 = head2;
if (ptr1 == NULL || ptr2 == NULL) {
return NULL;
}
while (ptr1 != ptr2) {
ptr1 = ptr1->next;
ptr2 = ptr2->next;
if (ptr1 == ptr2) {
return ptr1;
}
if (ptr1 == NULL) {
ptr1 = head2;
}
if (ptr2 == NULL) {
ptr2 = head1;
}
}
return ptr1;
}
void print(Node* node)
{
if (node == NULL)
cout << "NULL" ;
while (node->next != NULL) {
cout << node->data << "->" ;
node = node->next;
}
cout << node->data;
}
int main()
{
Node* newNode;
Node* head1 = new Node();
head1->data = 10;
Node* head2 = new Node();
head2->data = 3;
newNode = new Node();
newNode->data = 6;
head2->next = newNode;
newNode = new Node();
newNode->data = 9;
head2->next->next = newNode;
newNode = new Node();
newNode->data = 15;
head1->next = newNode;
head2->next->next->next = newNode;
newNode = new Node();
newNode->data = 30;
head1->next->next = newNode;
head1->next->next->next = NULL;
Node* intersect_node = NULL;
intersect_node = intersectPoint(head1, head2);
cout << "INTERSEPOINT LIST :" ;
print(intersect_node);
return 0;
}
Java
import java.util.*;
class GFG{
static class Node {
int data;
Node next;
};
static Node intersectPoint(Node head1, Node head2)
{
Node ptr1 = head1;
Node ptr2 = head2;
if (ptr1 == null || ptr2 == null ) {
return null ;
}
while (ptr1 != ptr2) {
ptr1 = ptr1.next;
ptr2 = ptr2.next;
if (ptr1 == ptr2) {
return ptr1;
}
if (ptr1 == null ) {
ptr1 = head2;
}
if (ptr2 == null ) {
ptr2 = head1;
}
}
return ptr1;
}
static void print(Node node)
{
if (node == null )
System.out.print( "null" );
while (node.next != null ) {
System.out.print(node.data+ "." );
node = node.next;
}
System.out.print(node.data);
}
public static void main(String[] args)
{
Node newNode;
Node head1 = new Node();
head1.data = 10 ;
Node head2 = new Node();
head2.data = 3 ;
newNode = new Node();
newNode.data = 6 ;
head2.next = newNode;
newNode = new Node();
newNode.data = 9 ;
head2.next.next = newNode;
newNode = new Node();
newNode.data = 15 ;
head1.next = newNode;
head2.next.next.next = newNode;
newNode = new Node();
newNode.data = 30 ;
head1.next.next = newNode;
head1.next.next.next = null ;
Node intersect_node = null ;
intersect_node = intersectPoint(head1, head2);
System.out.print( "INTERSEPOINT LIST :" );
print(intersect_node);
}
}
C#
using System;
public class GFG {
public
class Node {
public
int data;
public
Node next;
};
static Node intersectPoint(Node head1, Node head2) {
Node ptr1 = head1;
Node ptr2 = head2;
if (ptr1 == null || ptr2 == null ) {
return null ;
}
while (ptr1 != ptr2) {
ptr1 = ptr1.next;
ptr2 = ptr2.next;
if (ptr1 == ptr2) {
return ptr1;
}
if (ptr1 == null ) {
ptr1 = head2;
}
if (ptr2 == null ) {
ptr2 = head1;
}
}
return ptr1;
}
static void print(Node node) {
if (node == null )
Console.Write( "null" );
while (node.next != null ) {
Console.Write(node.data + "->" );
node = node.next;
}
Console.Write(node.data);
}
public static void Main(String[] args)
{
Node newNode;
Node head1 = new Node();
head1.data = 10;
Node head2 = new Node();
head2.data = 3;
newNode = new Node();
newNode.data = 6;
head2.next = newNode;
newNode = new Node();
newNode.data = 9;
head2.next.next = newNode;
newNode = new Node();
newNode.data = 15;
head1.next = newNode;
head2.next.next.next = newNode;
newNode = new Node();
newNode.data = 30;
head1.next.next = newNode;
head1.next.next.next = null ;
Node intersect_node = null ;
intersect_node = intersectPoint(head1, head2);
Console.Write( "INTERSEPOINT LIST :" );
print(intersect_node);
}
}
Output
INTERSEPOINT LIST :15->30
Time complexity : O( m + n )
Auxiliary Space: O(1)
Please write comments if you find any bug in the above algorithm or a better way to solve the same problem.
Find Merge Point of Two Lists Hackerrank Solution C++
Source: https://www.geeksforgeeks.org/write-a-function-to-get-the-intersection-point-of-two-linked-lists/